Volume 2, Issue 4 (November 2023)
Health Science Monitor 2023, 2(4): 225-232 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Kazempour Dizaji M, Emamhadi M A, Roozbahani R, Varahram M, Abedini A, Zare A, et al . Investigating the effect of health measures and social restrictions on the COVID-19 epidemic based on the SIQR mathematical model. Health Science Monitor 2023; 2 (4) :225-232
URL: http://hsm.umsu.ac.ir/article-1-104-en.html
URL: http://hsm.umsu.ac.ir/article-1-104-en.html
Mehdi Kazempour Dizaji * 

 , Mohammad Ali Emamhadi
, Mohammad Ali Emamhadi 

 , Rahim Roozbahani
, Rahim Roozbahani 

 , Mohammad Varahram
, Mohammad Varahram 

 , Atefe Abedini
, Atefe Abedini 

 , Ali Zare
, Ali Zare 

 , Arda Kiani
, Arda Kiani 

 , Niloufar Alizedeh Kolahdozi
, Niloufar Alizedeh Kolahdozi 

 , Syeyd Alireza Nadji
, Syeyd Alireza Nadji 

 , Majid Marjani
, Majid Marjani 




 , Mohammad Ali Emamhadi
, Mohammad Ali Emamhadi 

 , Rahim Roozbahani
, Rahim Roozbahani 

 , Mohammad Varahram
, Mohammad Varahram 

 , Atefe Abedini
, Atefe Abedini 

 , Ali Zare
, Ali Zare 

 , Arda Kiani
, Arda Kiani 

 , Niloufar Alizedeh Kolahdozi
, Niloufar Alizedeh Kolahdozi 

 , Syeyd Alireza Nadji
, Syeyd Alireza Nadji 

 , Majid Marjani
, Majid Marjani 


Mycobacteriology Research Center (MRC), National Research Institute of Tuberculosis and Lung Disease (NRITLD), Shahid Beheshti University of Medical Sciences, Tehran, Iran (Corresponding Author)
Keywords: COVID-19, Epidemic, Health measures, Mathematical modeling, SIQR model, Social restrictions
Full-Text [PDF 358 kb]
(658 Downloads)
| Abstract (HTML) (2436 Views)
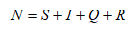
The outbreak of COVID-19 in China and the spread of the disease worldwide have posed a significant international challenge (5). The United States has suffered the most in this epidemic, with a quarter of all cases and a third of the mortality rate in the world (22). Russia, Brazil, and the United Kingdom are also the second to fourth countries affected by the COVID-19 epidemic (3, 23), and Spain, Italy, and Germany fifth to eighth, respectively (3, 22). Countries are trying to control the prevalence of the COVID-19 epidemic by observing health measures and imposing widespread social restrictions, as well as by different studies on medicines, treatment, and vaccines against the disease, to achieve effective methods for the treatment and prevention of COVID-19 (9-10, 12, 24).
So far, a specific treatment and medication have not been provided for this disease, and the only way to control this epidemic is to pay attention to health measures and social restrictions (5, 10, 14, 25). What level of health measures and social restrictions are needed to control the COVID-19 epidemic is a matter of the economic and social structure of each country. However, the positive role of health measures and social restrictions in controlling the COVID-19 epidemic needs to be emphasized (25, 26). Given that many aspects of COVID-19 (both the source of the disease and its treatment) are still unknown, simulation based on the mathematical models is the best way to understand the role of health measures and social restrictions on the outbreak of COVID-19 (17, 19-21). In this study, based on the SIQR mathematical model, the effect of different levels of health measures and social restrictions on the prevalence of the COVID-19 was investigated. Based on the results of this study, two points are very important. The first point is that with increasing the level of health measures and social restrictions, the rate of COVID-19 decreases. In this condition, fewer people in the community will be infected during the epidemic, and the number of identified (or quarantined) patients will be closer to the actual number of patients in the community. Also, as the epidemic time lengthens, and the number of infected patients decreases, there will be a good opportunity for researchers to find the time and money needed for clinical research to discover effective drugs or to produce a COVID-19 vaccine. Conversely, as the level of health measures and social restrictions decreases, the reproductive rate of COVID-19 will increase. In this case, more people in the community will be infected during the epidemic, and the number of identified (or quarantined) patients will be very different from the actual number of patients in the community. Following the shortening of the epidemic time and the increase in the morbidity and mortality rate of the COVID-19, the socio-economic structure and also the health care system of the country will face a crisis.
The second point that can be deduced from the results of this study is that with increasing the level of health measures and social restrictions, although the epidemic period increases, due to the presence of a small number of COVID-19 patients in the community, the disease will be controlled in the first phase. Moreover, the possibility of the second phase of this epidemic is very low and unlikely. However, with the reduction of health measures and social restrictions, while the duration of the epidemic period will be shorter, due to the large number of patients in the community, the epidemic of COVID-19 will not be controlled in the first phase, and the possibility of the second phase will be very high and probable. Therefore, the epidemic of COVID-19 can be controlled, and the recurrence of the disease and the formation of the second phase can be prevented by application of health measures by people in the community (e.g. wearing masks and gloves, and regular handwashing) and the application of social restrictions by governments (e.g. social distancing, closure of educational, cultural, and religious centers, and reduction of urban and interurban traffic). Of course, each country can choose the appropriate level of health measures and social restrictions to control COVID-19, depending on its economic strength, social structure, and the ability of its health care system. To achieve the desired result, there must be health and social restrictions to reduce the reproductive rate of COVID-19 to less than one.
Conclusion
The study of the impact of health measures and social restrictions on the COVID-19 epidemic using mathematical models such as the SIQR model will provide appropriate information on the disease spread. Also, it will help researchers select the appropriate level of these health measures and social restrictions to prevent the further spread of COVID-19.
Acknowledgments
None declared.
Conflict of interest
The authors have no conflict of interest in this study.
Funding/support
None declared.
Data availability
The raw data supporting the conclusions of this article are available from the authors upon reasonable request.
Full-Text: (941 Views)
Introduction
COVID-19 has been spreading from Wuhan, China, since December 2019 and is growing rapidly, leading to an epidemic in China and eventually a pandemic in other parts of the world (1, 2). To date, more than 10 million people worldwide have been diagnosed with COVID-19, and this trend is increasing (3). The spread of the COVID-19 virus is currently the most important global health challenge. Coronavirus includes a large family of viruses, consisting of seven different species, which are commonly found in both humans and animals (4). Some types of coronavirus, such as the virus causes COVID-19, can infect humans through animals and spread through human-to-human transmissions (5). Although this virus is less dangerous in terms of mortality than other emerging viruses of the corona family such as SARS and MERS, it has shown rapid spread and special pathogenic behaviors that make its control very difficult (6-8). The most common and severe manifestation of COVID-19 infection is pneumonia. Patients who suffer from COVID-19 often develop symptoms, on average, five days after the onset of the disease (9, 10). About 85% of these patients experience mild to moderate and approximately 15% have severe symptoms (10, 11). While some medications and treatments have been proposed for COVID-19, they are still in the experimental phase. Moreover, the efficacy of drugs for the treatment of patients with COVID-19 is unknown (12-15). Given the importance of COVID-19 from various aspects of personal and social health, the World Health Organization has recommended attention to health measures at the individual and community level and application of social restrictions by governments as the only appropriate strategy for COVID-19 epidemic control (5, 10). However, the effectiveness of these health measures and social restrictions in controlling the COVID-19 epidemic is unclear.
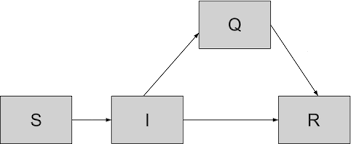
So far, no comprehensive study has been conducted to determine what level of health measures and social restrictions are needed to control, and how these measures will affect this epidemic. Simulation is an approach helps understand how the disease spreads and also study the impact of health measures and social restrictions on its control (8). In fact, simulation is a method that uses mathematical models to study the behavior of disease under different conditions (16). There are several mathematical models to simulate the COVID-19 epidemic pattern (17, 18). However, as the susceptible-infectious-quarantine-recovered (SIQR) model divides patients in the community into quarantined patients (Q) and unidentified patients (I), it is able to create a better understanding of this epidemic and also show more compatibility with the reality of the disease in the community (19). The SIQR model is one of the most common models for studying and simulating the epidemic of infectious diseases. In this model, people in the community are divided into four categories: people at risk (S), unidentified patients (I), quarantined patients (Q), and people who have recovered or died from the disease (R) (19). The model also assumes that everyone in the community is susceptible to and can suffer from the disease. Any infected person can infect the susceptible people, and after the susceptible person becomes infected, this person places into two categories of unidentified patients or quarantined patients. Any infected person (whether unidentified or quarantined) will be transferred to the recovered (R) group if they recover or die. This model contains four basic components, as follows:
• S: Number of susceptible people
• I: Number of infected and unidentified patients
• Q: Number of infected and quarantined patients
• R: Number of people who have recovered or died from the disease
Therefore, if we consider “N" the total population, "S" the population at risk, "I" the unidentified patients, "Q" the quarantined patients, and "R" the population who were recovered or dead, the simple formula for this model is as follows:
COVID-19 has been spreading from Wuhan, China, since December 2019 and is growing rapidly, leading to an epidemic in China and eventually a pandemic in other parts of the world (1, 2). To date, more than 10 million people worldwide have been diagnosed with COVID-19, and this trend is increasing (3). The spread of the COVID-19 virus is currently the most important global health challenge. Coronavirus includes a large family of viruses, consisting of seven different species, which are commonly found in both humans and animals (4). Some types of coronavirus, such as the virus causes COVID-19, can infect humans through animals and spread through human-to-human transmissions (5). Although this virus is less dangerous in terms of mortality than other emerging viruses of the corona family such as SARS and MERS, it has shown rapid spread and special pathogenic behaviors that make its control very difficult (6-8). The most common and severe manifestation of COVID-19 infection is pneumonia. Patients who suffer from COVID-19 often develop symptoms, on average, five days after the onset of the disease (9, 10). About 85% of these patients experience mild to moderate and approximately 15% have severe symptoms (10, 11). While some medications and treatments have been proposed for COVID-19, they are still in the experimental phase. Moreover, the efficacy of drugs for the treatment of patients with COVID-19 is unknown (12-15). Given the importance of COVID-19 from various aspects of personal and social health, the World Health Organization has recommended attention to health measures at the individual and community level and application of social restrictions by governments as the only appropriate strategy for COVID-19 epidemic control (5, 10). However, the effectiveness of these health measures and social restrictions in controlling the COVID-19 epidemic is unclear.
So far, no comprehensive study has been conducted to determine what level of health measures and social restrictions are needed to control, and how these measures will affect this epidemic. Simulation is an approach helps understand how the disease spreads and also study the impact of health measures and social restrictions on its control (8). In fact, simulation is a method that uses mathematical models to study the behavior of disease under different conditions (16). There are several mathematical models to simulate the COVID-19 epidemic pattern (17, 18). However, as the susceptible-infectious-quarantine-recovered (SIQR) model divides patients in the community into quarantined patients (Q) and unidentified patients (I), it is able to create a better understanding of this epidemic and also show more compatibility with the reality of the disease in the community (19). The SIQR model is one of the most common models for studying and simulating the epidemic of infectious diseases. In this model, people in the community are divided into four categories: people at risk (S), unidentified patients (I), quarantined patients (Q), and people who have recovered or died from the disease (R) (19). The model also assumes that everyone in the community is susceptible to and can suffer from the disease. Any infected person can infect the susceptible people, and after the susceptible person becomes infected, this person places into two categories of unidentified patients or quarantined patients. Any infected person (whether unidentified or quarantined) will be transferred to the recovered (R) group if they recover or die. This model contains four basic components, as follows:
• S: Number of susceptible people
• I: Number of infected and unidentified patients
• Q: Number of infected and quarantined patients
• R: Number of people who have recovered or died from the disease
Therefore, if we consider “N" the total population, "S" the population at risk, "I" the unidentified patients, "Q" the quarantined patients, and "R" the population who were recovered or dead, the simple formula for this model is as follows:
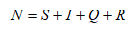
The SIQR model is suitable for predicting infectious diseases transmitted from human to human, as well as recovering patients who are resistant to re-infection.

Fig. 1. Schematic of the SIQR mathematical model for COVID-19.
The SIQR model consists of three basic parameters, r, γ, and β, which need to be determined according to the type of disease and the different scenarios that the researcher considers for the disease. The parameter r is the reproductive rate of the disease and is related to the pathogenicity of the infectious agent. This parameter is strongly influenced by health measures and social restrictions; in other words, it is related to the incidence rate. The parameter γ determines the recovery rate of the disease and is influenced by treatment measures and vaccines. The parameter β determines the quarantine rate or disease detection rate, which is affected by the ability of the health care system to identify patients. The disease prevalence, reproduction rate, recovery rate, and disease detection rate or quarantine is important determining factors. Each disease has its own reproductive rate, which, apparently, this parameter in COVID-19 is a large number of about 2.2 to 2.5 (10). The values of this parameter can be controlled by applying social restrictions and quarantine. If α is considered the extent of social and health restrictions for disease control, the reproductive rate can be controlled as r (1- α). In this regard, α = 1 denotes the application of 100% restrictions in society, and α = 0 means no health measures are taken, and no social restrictions are imposed on disease control.
Due to the fact that there is no specific treatment and vaccine are available for COVID-19, the parameter of the recovery rate (γ) was considered constant, and based on the ability of the health system of countries was assumed about 0.5 to 0.7 (20, 21). The parameter of quarantine or disease detection rate (β) is more related to the medical system. Since the actual number of patients in the community is 10 to 20 times higher than the official statistics, this parameter was considered constant and about 0.1 to 0.2 (16, 21). Therefore, in the study of the COVID-19 epidemic, reproductive rate (r) is the only parameter that changes under the influence of health measures and social restrictions. The changes or dynamics of the number of people in each group can be expressed over time using differential equations mathematically, and the status of the disease can be assessed using simulations. This study aimed to investigate the impact of health measures by the people and social restrictions by the government on the COVID-19 epidemic, based on the SIQR model.
Materials & Methods
In this study, the effect of health measures and social restrictions on the COVID-19 epidemic was investigated based on the SIQR mathematical model. The present study hypothesized that the recovery and quarantine rates (or the detection rate) was constant because the values of these two parameters depended on the ability of the health care system to treat COVID-19 and identify patients (especially asymptomatic patients, and patients with mild to moderate symptoms), as well as vaccine discovery. Given that the reproductive rate is the only parameter in the SIQR model that was dependent on the health measures and social restrictions, the role of health measures and social constraints on the COVID-19 epidemic was investigated based on changes of this parameter.
To estimate the parameters of SIQR model, we used the information of COVID-19 patients who referred to Dr. Masih Daneshvari Hospital in Tehran (Iran) during the epidemic of the disease, statistics and daily information on COVID-19 epidemic reported by the Iran’s Ministry of Health and Medical Education, and the results of other studies related to COVID-19. It should be noted that the population considered in this study was about 100 million people. MATLAB software was used to study the effect of health measures and social restrictions on the COVID-19 epidemic.
Results
Given that the reproduction rate (r) is the only parameter depending on health measures and social restrictions in the SIQR model, the parameters recovery rate (γ) and quarantine or disease detection rate (β) were considered constant and equal to 0.7 and 0. 2, respectively.
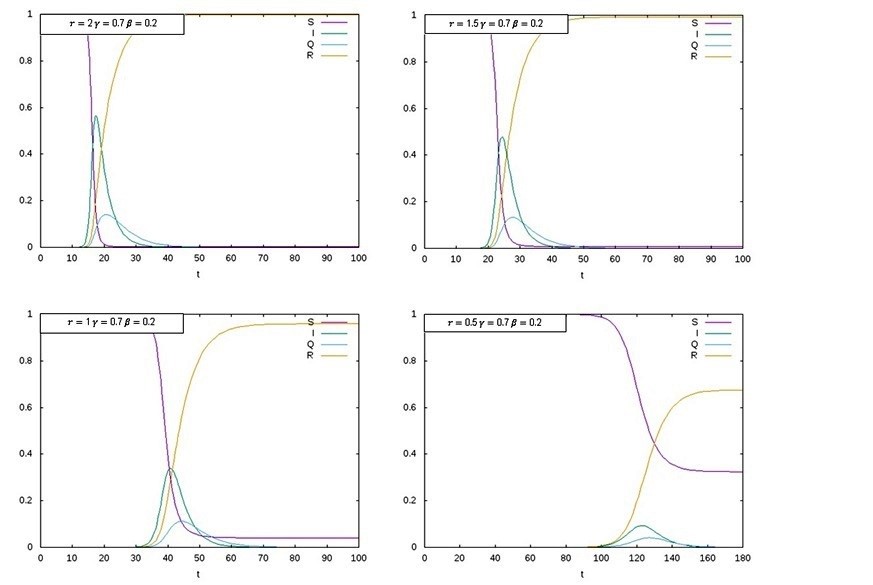
Based on the level of health measures and also social restrictions equivalent to 80, 60, 40, and 20%, the reproductive rate parameter reduced from 2.5 to 0.5, 1, 1.5, and 2, respectively (Figure 1). The results of the SIQR model indicated a level of 20% for both health measures and social restrictions and the rate of 2 for COVID-19 reproduction. According to the results of this simulation, the disease reached its peak 20 days from the start of the epidemic, and nearly 60% of the population (60 million people) was affected by this disease (Figure 2). Also, the number of identified (or quarantined) patients was very different from the number of real patients in the community. As the results of this study showed, all people in the community were exposed to this disease until the end of the initial phase of the COVID-19 epidemic.
With the increased level of health measures and social restrictions to 40%, the rate of reproduction of COVID-19 reached 1.5. In this case, it reached its peak in about 25 days from the beginning of the epidemic, and about 50% of the population (50 million people) was affected (Figure 2). At this level of health measures and social restrictions, the number of identified (or quarantined) patients was still very different from the number of real patients in the community, and by the end of the initial phase of the COVID-19 epidemic, all the members of the community were exposed to this disease.
With an increase in the level of health measures and social restrictions to 60%, the rate of reproduction of COVID-19 decreased to 1, which in this case, it reached the peak after 40-45 days from the beginning of the epidemic, and about 35% of the community (35 million people) was affected (Figure 2). At this level of health measures and social restrictions, the number of identified (or quarantined) patients was closer to the number of real patients in the community, and by the end of the initial phase of the COVID-19 epidemic, about 95% of the population was at risk. In other words, according to the results of the SIQR model, about 5% of the population was not affected by the disease.
According to the increased level of health measures and social restrictions to 80%, the rate of reproduction of COVID-19 reached 0.5. However, after 120 to 125 days from the beginning of the epidemic, the peak of the disease epidemic was about 10% of the population (10 million people) (Figure 2). At this level of health measures and social restrictions, the number of identified (or quarantined) patients was very close to the number of real patients in the community, and by the end of the initial phase of the COVID-19 epidemic, about 75% of the population was exposed to the diseases. In other words, about 35% of the population was affected by COVID-19.
Due to the fact that there is no specific treatment and vaccine are available for COVID-19, the parameter of the recovery rate (γ) was considered constant, and based on the ability of the health system of countries was assumed about 0.5 to 0.7 (20, 21). The parameter of quarantine or disease detection rate (β) is more related to the medical system. Since the actual number of patients in the community is 10 to 20 times higher than the official statistics, this parameter was considered constant and about 0.1 to 0.2 (16, 21). Therefore, in the study of the COVID-19 epidemic, reproductive rate (r) is the only parameter that changes under the influence of health measures and social restrictions. The changes or dynamics of the number of people in each group can be expressed over time using differential equations mathematically, and the status of the disease can be assessed using simulations. This study aimed to investigate the impact of health measures by the people and social restrictions by the government on the COVID-19 epidemic, based on the SIQR model.
Materials & Methods
In this study, the effect of health measures and social restrictions on the COVID-19 epidemic was investigated based on the SIQR mathematical model. The present study hypothesized that the recovery and quarantine rates (or the detection rate) was constant because the values of these two parameters depended on the ability of the health care system to treat COVID-19 and identify patients (especially asymptomatic patients, and patients with mild to moderate symptoms), as well as vaccine discovery. Given that the reproductive rate is the only parameter in the SIQR model that was dependent on the health measures and social restrictions, the role of health measures and social constraints on the COVID-19 epidemic was investigated based on changes of this parameter.
To estimate the parameters of SIQR model, we used the information of COVID-19 patients who referred to Dr. Masih Daneshvari Hospital in Tehran (Iran) during the epidemic of the disease, statistics and daily information on COVID-19 epidemic reported by the Iran’s Ministry of Health and Medical Education, and the results of other studies related to COVID-19. It should be noted that the population considered in this study was about 100 million people. MATLAB software was used to study the effect of health measures and social restrictions on the COVID-19 epidemic.
Results
Given that the reproduction rate (r) is the only parameter depending on health measures and social restrictions in the SIQR model, the parameters recovery rate (γ) and quarantine or disease detection rate (β) were considered constant and equal to 0.7 and 0. 2, respectively.
Based on the level of health measures and also social restrictions equivalent to 80, 60, 40, and 20%, the reproductive rate parameter reduced from 2.5 to 0.5, 1, 1.5, and 2, respectively (Figure 1). The results of the SIQR model indicated a level of 20% for both health measures and social restrictions and the rate of 2 for COVID-19 reproduction. According to the results of this simulation, the disease reached its peak 20 days from the start of the epidemic, and nearly 60% of the population (60 million people) was affected by this disease (Figure 2). Also, the number of identified (or quarantined) patients was very different from the number of real patients in the community. As the results of this study showed, all people in the community were exposed to this disease until the end of the initial phase of the COVID-19 epidemic.
With the increased level of health measures and social restrictions to 40%, the rate of reproduction of COVID-19 reached 1.5. In this case, it reached its peak in about 25 days from the beginning of the epidemic, and about 50% of the population (50 million people) was affected (Figure 2). At this level of health measures and social restrictions, the number of identified (or quarantined) patients was still very different from the number of real patients in the community, and by the end of the initial phase of the COVID-19 epidemic, all the members of the community were exposed to this disease.
With an increase in the level of health measures and social restrictions to 60%, the rate of reproduction of COVID-19 decreased to 1, which in this case, it reached the peak after 40-45 days from the beginning of the epidemic, and about 35% of the community (35 million people) was affected (Figure 2). At this level of health measures and social restrictions, the number of identified (or quarantined) patients was closer to the number of real patients in the community, and by the end of the initial phase of the COVID-19 epidemic, about 95% of the population was at risk. In other words, according to the results of the SIQR model, about 5% of the population was not affected by the disease.
According to the increased level of health measures and social restrictions to 80%, the rate of reproduction of COVID-19 reached 0.5. However, after 120 to 125 days from the beginning of the epidemic, the peak of the disease epidemic was about 10% of the population (10 million people) (Figure 2). At this level of health measures and social restrictions, the number of identified (or quarantined) patients was very close to the number of real patients in the community, and by the end of the initial phase of the COVID-19 epidemic, about 75% of the population was exposed to the diseases. In other words, about 35% of the population was affected by COVID-19.

Fig. 2. Effect of the health measures and social restrictions on the COVID-19 epidemic based on the SIQR model by considering the reproductive rate (r), constant values for the recovery rate (γ), and quarantine or disease detection rate (β).
DiscussionThe outbreak of COVID-19 in China and the spread of the disease worldwide have posed a significant international challenge (5). The United States has suffered the most in this epidemic, with a quarter of all cases and a third of the mortality rate in the world (22). Russia, Brazil, and the United Kingdom are also the second to fourth countries affected by the COVID-19 epidemic (3, 23), and Spain, Italy, and Germany fifth to eighth, respectively (3, 22). Countries are trying to control the prevalence of the COVID-19 epidemic by observing health measures and imposing widespread social restrictions, as well as by different studies on medicines, treatment, and vaccines against the disease, to achieve effective methods for the treatment and prevention of COVID-19 (9-10, 12, 24).
So far, a specific treatment and medication have not been provided for this disease, and the only way to control this epidemic is to pay attention to health measures and social restrictions (5, 10, 14, 25). What level of health measures and social restrictions are needed to control the COVID-19 epidemic is a matter of the economic and social structure of each country. However, the positive role of health measures and social restrictions in controlling the COVID-19 epidemic needs to be emphasized (25, 26). Given that many aspects of COVID-19 (both the source of the disease and its treatment) are still unknown, simulation based on the mathematical models is the best way to understand the role of health measures and social restrictions on the outbreak of COVID-19 (17, 19-21). In this study, based on the SIQR mathematical model, the effect of different levels of health measures and social restrictions on the prevalence of the COVID-19 was investigated. Based on the results of this study, two points are very important. The first point is that with increasing the level of health measures and social restrictions, the rate of COVID-19 decreases. In this condition, fewer people in the community will be infected during the epidemic, and the number of identified (or quarantined) patients will be closer to the actual number of patients in the community. Also, as the epidemic time lengthens, and the number of infected patients decreases, there will be a good opportunity for researchers to find the time and money needed for clinical research to discover effective drugs or to produce a COVID-19 vaccine. Conversely, as the level of health measures and social restrictions decreases, the reproductive rate of COVID-19 will increase. In this case, more people in the community will be infected during the epidemic, and the number of identified (or quarantined) patients will be very different from the actual number of patients in the community. Following the shortening of the epidemic time and the increase in the morbidity and mortality rate of the COVID-19, the socio-economic structure and also the health care system of the country will face a crisis.
The second point that can be deduced from the results of this study is that with increasing the level of health measures and social restrictions, although the epidemic period increases, due to the presence of a small number of COVID-19 patients in the community, the disease will be controlled in the first phase. Moreover, the possibility of the second phase of this epidemic is very low and unlikely. However, with the reduction of health measures and social restrictions, while the duration of the epidemic period will be shorter, due to the large number of patients in the community, the epidemic of COVID-19 will not be controlled in the first phase, and the possibility of the second phase will be very high and probable. Therefore, the epidemic of COVID-19 can be controlled, and the recurrence of the disease and the formation of the second phase can be prevented by application of health measures by people in the community (e.g. wearing masks and gloves, and regular handwashing) and the application of social restrictions by governments (e.g. social distancing, closure of educational, cultural, and religious centers, and reduction of urban and interurban traffic). Of course, each country can choose the appropriate level of health measures and social restrictions to control COVID-19, depending on its economic strength, social structure, and the ability of its health care system. To achieve the desired result, there must be health and social restrictions to reduce the reproductive rate of COVID-19 to less than one.
Conclusion
The study of the impact of health measures and social restrictions on the COVID-19 epidemic using mathematical models such as the SIQR model will provide appropriate information on the disease spread. Also, it will help researchers select the appropriate level of these health measures and social restrictions to prevent the further spread of COVID-19.
Acknowledgments
None declared.
Conflict of interest
The authors have no conflict of interest in this study.
Funding/support
None declared.
Data availability
The raw data supporting the conclusions of this article are available from the authors upon reasonable request.
Type of Study: Research |
Subject:
General
Received: 2022/12/25 | Accepted: 2023/01/4 | Published: 2023/10/29
Received: 2022/12/25 | Accepted: 2023/01/4 | Published: 2023/10/29
References
1. Gao J, Tian Z, Yang X. Breakthrough: Chloroquine phosphate has shown apparent efficacy in treatment of COVID-19 associated pneumonia in clinical studies. Biosci Trends. 2020;14(1):72-73. doi:10.5582/bst.2020.01047. [DOI] [PMID]
2. Hui DS, Azhar EI, Madani TA, Ntoumi F, Kock R, Dar O, et al. The continuing 2019-nCoV epidemic threat of novel coronaviruses to global health - The latest 2019 novel coronavirus outbreak in Wuhan, China. Int J Infect Dis. 2020;91:264-266. doi:10.1016/j.ijid.2020.01.009. [DOI] [PMID] [PMCID]
3. COVID-19 Dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). ArcGIS [Internet]. Johns Hopkins University; 2020 [cited 2020 May 26]. Available from: https://coronavirus.jhu.edu/map.html. [URL]
4. Roush S, Birkhead G, Koo D, Cobb L, Fleming D; Centers for Disease Control and Prevention (CDC). National Center for Immunization and Respiratory Diseases (NCIRD) Support for Modernization of the Nationally Notifiable Diseases Surveillance System (NNDSS) to Strengthen Public Health Surveillance Infrastructure in the US [abstract]. In: 2019 CSTE Annual Conference; 2019 Jun 2-6; Raleigh, NC. [URL]
5. World Health Organization (WHO). WHO Director-General's remarks at the media briefing on 2019-nCoV on 11 February 2020 [Internet]. Geneva: WHO; 2020 [cited 2020 Feb 11]. Available from: https://www.who.int/director-general/speeches/detail/who-director-general-s-remarks-at-the-media-briefing-on-2019-ncov-on-11-february-2020. [URL]
6. Maitra S, Biswas M, Bhattacharjee S. Case-fatality rate in COVID-19 patients: A meta-analysis of publicly accessible database [preprint]. medRxiv [Internet]. 2020 [cited 2020 May 26]. Available from: https://www.medrxiv.org/content/10.1101/2020.05.22.20109231v1. [DOI]
7. Wu Z, McGoogan JM. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: summary of a report of 72 314 cases from the Chinese Center for Disease Control and Prevention. JAMA. 2020;323(13):1239-1242. doi:10.1001/jama.2020.2648. [DOI] [PMID]
8. Mahase E. Coronavirus: covid-19 has killed more people than SARS and MERS combined, despite lower case fatality rate [news]. BMJ [Internet]. 2020 Feb 18 [cited 2020 May 26];368:m641. Available from: https://www.bmj.com/content/368/bmj.m641. [DOI] [PMID]
9. Guan W-j, Ni Z-y, Hu Y, Liang W-h, Ou C-q, He J-x, et al.; China Medical Treatment Expert Group for Covid-19. Clinical characteristics of coronavirus disease 2019 in China [published online ahead of print February 28, 2020]. N Engl J Med [Internet]. doi:10.1056/NEJMoa2002032. [DOI] [PMID] [PMCID]
10. Li Q, Guan X, Wu P, Wang X, Zhou L, Tong Y, et al.; Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia Investigation Team*. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia [published online ahead of print January 29, 2020]. N Engl J Med [Internet]. doi:10.1056/NEJMoa2001316. [DOI] [PMID] [PMCID]
11. Chan JF-W, Yuan S, Kok K-H, To KK-W, Chu H, Yang J, et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395(10223):514-523. doi:10.1016/S0140-6736(20)30154-9. [DOI] [PMID]
12. Li G, De Clercq E. Therapeutic options for the 2019 novel coronavirus (2019-nCoV). Nat Rev Drug Discov. 2020;19(3):149-150. doi:10.1038/d41573-020-00016-0. [DOI] [PMID]
13. Ahn JY, Sohn Y, Lee SH, Cho Y, Hyun JH, Baek YJ, et al. Use of convalescent plasma therapy in two COVID-19 patients with acute respiratory distress syndrome in Korea. J Korean Med Sci. 2020;35(14):e149. doi:10.3346/jkms.2020.35.e149. [DOI] [PMID] [PMCID]
14. Lu H. Drug treatment options for the 2019-new coronavirus (2019-nCoV). Biosci Trends. 2020;14(1):69-71. doi:10.5582/bst.2020.01020. [DOI] [PMID]
15. Tanne JH. Covid-19: FDA approves use of convalescent plasma to treat critically ill patients [news]. BMJ [Internet]. 2020 Mar 26 [cited 2020 May 26];368:m1256. Available from: https://www.bmj.com/content/368/bmj.m1256. [DOI] [PMID]
16. Nesteruk I. Estimations of the coronavirus epidemic dynamics in south korea with the use of sir model [preprint]. ResearchGate [Internet]. 2020 Mar [cited 2020 May 26]. Available from: https://www.researchgate.net/publication/339961786_Estimations_of_the_coronavirus_epidemic_dynamics_in_South_Korea_with_the_use_of_SIR_model. [URL]
17. Chen Y-C, Lu P-E, Chang C-S. A time-dependent SIR model for COVID-19 [preprint]. arXiv [Internet]. 2020 Mar 2 [cited 2020 May 26]. Available from: https://arxiv.org/abs/2003.00122. [URL]
18. Zhu K, Ying L. Information source detection in the SIR model: A sample-path-based approach. IEEE/ACM Trans Netw [Internet]. 2016 Feb;24(1):408-421. doi:10.1109/TNET.2014.2369495. [DOI]
19. Hethcote H, Zhien M, Shengbing L. Effects of quarantine in six endemic models for infectious diseases [abstract]. Math Biosci [Internet]. 2002 Jul;180(1-2):141-160. [DOI] [PMID]
20. Calafiore GC, Novara C, Possieri C. A modified SIR model for the COVID-19 contagion in Italy [preprint]. arXiv [Internet]. 2020 Mar 22 [cited 2020 May 26]. Available from: https://arxiv.org/abs/2003.14391. [DOI]
21. Peng L, Yang W, Zhang D, Zhuge C, Hong L. Epidemic analysis of COVID-19 in China by dynamical modeling [preprint]. arXiv [Internet]. 2020 Feb 15 [cited 2020 May 26]. Available from: https://arxiv.org/abs/2002.06563. [DOI]
22. COVID C. Global Cases by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. Coronavirus Resource Center [Internet]. Johns Hopkins University; 2020 Mar 17 [cited 2020 May 26]. Available from: https://coronavirus.jhu.edu/map.html. [URL]
23. Coronavirus COVID-19 Global Cases by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). ArcGIS [Internet]. Johns Hopkins University; 2020 [cited 2020 May 26]. Available from: https://gisanddata.maps.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6. [URL]
24. Singh R, Adhikari R. Age-structured impact of social distancing on the COVID-19 epidemic in India [preprint]. arXiv [Internet]. 2020 Mar 26 [cited 2020 May 26]. Available from: https://arxiv.org/abs/2003.12055. [URL]
25. Rothe C, Schunk M, Sothmann P, Bretzel G, Froeschl G, Wallrauch C, et al. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N Engl J Med. 2020;382(10):970-971. doi:10.1056/NEJMc2001468. [DOI] [PMID] [PMCID]
26. Kupferschmidt K. Study claiming new coronavirus can be transmitted by people without symptoms was flawed [news]. Science [Internet]. 2020 Feb 3 [cited 2020 May 26]. Available from: https://www.sciencemag.org/news/2020/02/paper-non-symptomatic-patient-transmitting-coronavirus-wrong [DOI]
Send email to the article author
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |




 gmail.com
gmail.com